About Lesson
2.2 Calculation of Inverse Trigonometric Functions
Find the value of the following statement
求下列各式的值
(1) ![Rendered by QuickLaTeX.com cos{[}{sin}^{-1}{(}-\frac{4}{5})-{cos}^{-1}{(}-\frac{3}{5})]](https://learn-ondemand.com/wp-content/ql-cache/quicklatex.com-9f0771276f6303f6cddfd4c698c553dc_l3.png)
Answer :
-1
(2) 
Answer :
(3) 
Answer :
(4) ![Rendered by QuickLaTeX.com tan{[}2{tan}^{-1}{\frac{1}{5}}-{cos}^{-1}{(}-\frac{8}{17})]](https://learn-ondemand.com/wp-content/ql-cache/quicklatex.com-9bda520b4af2fd8f2aacfeab5b9460df_l3.png)
Answer :
(5) 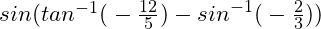
Answer :
(6) 
Answer :
(7) Given that  and
and 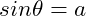 , find
, find 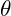 in terms of a.
in terms of a.
已知 和
和 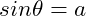 , 试用 a 表示
, 试用 a 表示 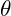 .
.
已知