Course Content
第1章：数学归纳法
0/1
1 Mathematical Induction 数学归纳法 [练习题]
第2章：反三角函数
0/3
2.2 Calculation of Inverse Trigonometric Functions
2.3 Inverse Trigonometry Function Identities 反三角函数的恒等式
2.4 Inverse Trigonometric Function Equations 反三角函数方程式
第3章：微分法（二）
0/5
3.2 Derivative of Inverse Trigonometric Functions
3.3 Derivative of Logarithm Functions 对数函数的导数
3.4 Derivative of Exponential Functions 指数函数的导数
3.5 Logarithmic Differentiation 对数微分法
3.6 L’Hospital’s Rule 罗比达法则
第4章：坐标变换
第5 章 圆锥曲线
0/3
5.2 Parabola 抛物线
5.3 Ellipse 椭圆
5.4 Hyperbola 双曲线
第7章：参数方程式
0/2
7.3 Parametric Equations and Locus 参数方程式与轨迹
7.5 Parametric Equations of Conic 圆锥曲线的参数方程式
第9章 复数
0/4
9.2 Complex Number and Its Evaluation复数及其运算
9.5 de Moivre’s Theorem 隶美佛定理
9.6 The nth Root of Complex Number 复数的n次方根
9.7 Roots of Unary nth Order Equations 一元n 次方程式的根
第10章 微分法的应用（二）
0/2
10.1 Graphing for Curve 曲线的作图法
10.2 The Approximate Solution of Unary Equations 一元方程式的近似解
第12章 定积分及其应用（二）
0/1
12.2 Calculation of Area under Polar Coordinate 极坐标系下的面积计算
第13章 常微分方程式
0/5
13.2 First Order Differential Equations 一阶微分方程
13.2.2 First Order Homogeneous Differential Equations 一阶齐次微分方程
13.2.3 First Order Linear Differential Equations 一阶线性微分方程
13.3 Application of First Order Differential Equations 一阶常微分方程的应用
13.4 Second Order Linear Differential Equation with Constant Coefficient 二阶常系数线性微分方程
高三数学 | 高级数学
About Lesson
5.3 Ellipse 椭圆

1. Find the centre, vertex, axis of symmetry, major semi-axis, minor semi-axis, eccentricity, focus, directrix and length of latus rectum for the following ellipse and sketch the graph.
求以下各椭圆的中心, 顶点, 对称轴, 半长轴之长, 半短轴之长, 离心率, 焦点, 准线和通径长度並描其图形

(a) \frac{x^2}{50}+\frac{y^2}{32}=2

(b) 25x^2 + 9y^2 = 225

(c) 4x^2 + y^2 + 16x- 10y- 23 = 0

(d) 4x^2+ 9y^2 - 16x + 18y - 11 = 0

(e) 25x^2 + 16y^2 -150x + 32y - 159 = 0

Answer (a) :

Answer (b) :

Answer (c) :

Answer (d) :

Answer (e) :

2. Find the equation of the ellipse with center at (-3, 1), one of vertices at (-5, 1), length of latus rectum equal to 1 and
求椭圆方程式其中心在(-3, 1), 其中一顶点在(-5, 1), 通径长度为1且

(a) major axis parallel x-axis,
长轴平行于x轴,

(b) major axis parallel y-axis,
长轴平行于y轴,

Answer :
(a) (x + 3)^2 + 4(y - 1)^2 = 4

(b) \frac{{(x+3)}^2}{4}+\frac{{(y-1)}^2}{64}=1

3. Find the equation of the ellipse which has same eccentricity and left directrix with ellipse x^2 + 2y^2 = 2, and also take its right focus to be the left focus.

求与椭圆x^2 + 2y^2 = 2有相同的离心率和公共的左准线,且以它的右焦点为左焦点的椭圆方程.

Answer :
\frac{{(x-4)}^2}{18}+\frac{y^2}{9}=1
4. Given that the major axis of an ellipse is 4, y-axis be its directrix, the left focus is on the parabola y^2 = x - 1. Find the equation of the ellipse when eccentricity is \frac{2}{3}.

己知椭圆的长轴长为4，以y轴为准线，左焦点在拋物线y^2 = x - 1上。求当离心率为\frac{2}{3}时, 此椭圆方程式。

Answer :
\frac{{(x-3)}^2}{4}+\frac{9{(y\pm\sqrt{2/3})}^2}{20}=100
5. Given that F_1(2, -2), F_2(2, 0) are the foci of a ellipse, straight line y = 3 is a directrix of the ellipse, find the equation of the ellipse.

已知椭圆的焦点为F_1(2, -2), F_2(2, 0), 直线y = 3是椭圆的一条准线, 求椭圆的方程.

Answer :
\frac{{(x-2)}^2}{3}+\frac{{(y+1)}^2}{4}=1
6. Find the equation of the ellipse with vertices at (0, -1) and (12, -1), a focus at 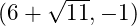(6 + \sqrt{11}, -1).

求顶点在 (0, -1) 和 (12, -1), 一焦点在 (6 + \sqrt{11}, -1) 的椭圆方程式

Answer :
\frac{{(x-6)}^2}{36}+\frac{{(y+1)}^2}{25}=1
Previous
Next