About Lesson
Solve the following trigonometric equations with given range of angle (1 ~ 11)
在所给的角度范围解下列各三角方程式(1 ~ 11)
在所给的角度范围解下列各三角方程式(1 ~ 11)
(1) ![]()
![]()
Answer:
(2) ![]()
![]()
Answer:
![]()
(3) ![]()
![]()
Answer:
![]()
(4) ![]()
![]()
Answer:
(5) 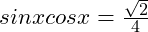
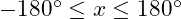
Answer:
22.5 , 67.5
, 67.5 , -112.5
, -112.5 , -157.5
, -157.5
(6) 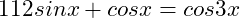
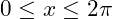
Answer:
0,  ,
,  ,
,  ,
, 
(7) 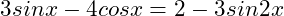
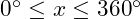
Answer:
41.81 , 120
, 120 , 138.19
, 138.19 , 240
, 240
(8) 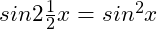
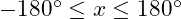
Answer:
0 , 120
, 120 , -120
, -120
(9) 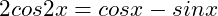
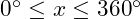
Answer:
45 , 114.3
, 114.3 , 225
, 225 , 335.7
, 335.7
(10) 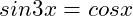
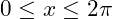
Answer:
(11) 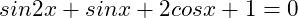
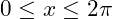
Answer:
Give the general solution of the following trigonometric equations. (12 ~ 17)
求下列各三角方程式的一般解(12 ~ 17)
求下列各三角方程式的一般解(12 ~ 17)
(12) 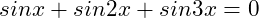
Answer:
(13) 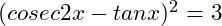
Answer:
(14) 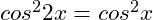
Answer:
(15) 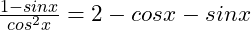
Answer:
(16) 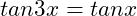
Answer:
(17) 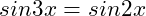
Answer:
Solve the following a sin x + b cos x = c trigonometric equations with given range of angle (18 ~ 21)
在所给的角度范围解下列a sin x + b cos x = c 的三角方程式(18 ~ 21)
在所给的角度范围解下列a sin x + b cos x = c 的三角方程式(18 ~ 21)
(18) ![]()
![]()
Answer:
(19) ![]()
![]()
Answer:
(20) ![]()
![]()
Answer:
45![]() , 161.57
, 161.57![]() , 225
, 225![]() , 341.57
, 341.57![]()
(21) 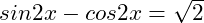
(一般解、general solution)
(一般解、general solution)
Answer:
(22) Express  in term of
in term of 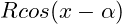 where R > 0 and
where R > 0 and 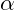 is acute angle. Find the values of R and \alpha. Hence,
is acute angle. Find the values of R and \alpha. Hence,
把 ![]() 用
用 ![]() 表示,其中 R > 0 且
表示,其中 R > 0 且 ![]() 为一锐角. 求 R 和
为一锐角. 求 R 和 ![]() 的值。据此
的值。据此
(a) write down the maximum value of ![]()
写下![]() 的最大值
的最大值
(b) solve the equation ![]() , where
, where ![]()
解方程式 ![]() , 其中
, 其中 ![]()
Answer:
(a) 2
(b) ![]() ,
, ![]()
(23) If 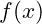 =
=  =
= 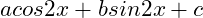 , find
, find
若 ![]() =
= ![]() =
= ![]() , 求
, 求
(a) the values of a, b and c,
a, b 和 c的值,
(b) the maximum and minimum values of ![]() ,
,
![]() 的最大和最小值
的最大和最小值
(c) the general solution of the equation ![]() .
.
![]() 的一般解
的一般解
Answer:
(a) 5, -12, 12
(b) -1, 25
(c) n·180![]() + 4.64
+ 4.64![]() , n·180
, n·180![]() – 72.02
– 72.02![]()