About Lesson
10.5 Graphical Solutions of Trigonometric Equations 三角方程式的图解法
(1) Sketch on the same diagram, the curves  and
and  for the interval
for the interval  . State the number of solutions in the interval
. State the number of solutions in the interval  of the equation
of the equation  .
.
在同一个图,描曲线 ![]() 和
和 ![]() 当
当 ![]() . 试说明在
. 试说明在 ![]() 的区间方程式
的区间方程式 ![]() 有多少个解.
有多少个解.
Answer :
4
(2) Sketch  and
and  for
for 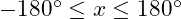 and find the number of solution for
and find the number of solution for 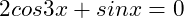 .
.
在![]() 中描
中描![]() 和
和 ![]() 且求
且求 ![]() 有多少个实数解。
有多少个实数解。
Answer :
6
(3) Find the number of solution for the equation  where
where  .
.
求在![]() 中,
中,![]() 有多少个实数解。
有多少个实数解。
Answer :
4
(4) Sketch the graph of  =
= for
for 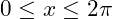 . By sketching a suitable straight line on the same diagram, find the number of solution for
. By sketching a suitable straight line on the same diagram, find the number of solution for  +
+ =
= .
.
描图 ![]() =
=![]() 当
当 ![]() . 在同一个图描一适当的直线,求
. 在同一个图描一适当的直线,求 ![]() +
+![]() =
=![]() 有多少个实数解有多少个实数解。
有多少个实数解有多少个实数解。
Answer :
5
(5) Sketch the graphs of  such that
such that 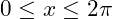 .
.
Hence, obtain the number of solutions of
Hence, obtain the number of solutions of
描图![]() 当
当 ![]() .
.
据此,找 ![]() 有多少个实数解
有多少个实数解
Answer :
4