About Lesson
11.4 Area of Poligons 多边形的面积
1. P(4, 2), Q(5, 6), R(x, y) and S(-4, 1) are the vertices of a parallelogram PQRS. Find
P(4, 2), Q(5, 6), R(x, y) 和 S(-4, 1) 是一平行四边形PQRS 的顶点, 求
(a) the coordinate of R,
R 的坐标
(b) the area of parallelogram PQRS.
平行四边形PQRS 的面积。
Answer :
(a) (–3,5)
(b) 31 unit![]()
2. ABCD is a rhombus that the coordinates of A, B, C and D are (3, -2), (p, 3), (q, r) and (6, 2) respectively. Calculate
ABCD 是一菱形且A, B, C 和 D 的坐标分别是 (3, -2), (p, 3), (q, r) 和 (6, 2)。求
(a) the values of p, q and r,
p, q 和r的值,
(b) the area of the rhombus.
菱形的面积
Answer :
(a) 3, 6, 7
(b) 15 unit![]()
3. Coordinates of the vertices A(4, 7), B(0, 5) and C(1, 6) of a triangle, and D is the midpoint of BC. Show that AB + AC
+ AC = 2AD
= 2AD +
+ 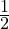 BC
BC . Find the area of the quadrilateral OABC, where O is the origin.
. Find the area of the quadrilateral OABC, where O is the origin.
一三角形的顶点坐标是A(4, 7), B(0, 5) and C(1, 6), 和 D 是 BC 的中点. 证明AB![]() + AC
+ AC![]() = 2AD
= 2AD![]() +
+ ![]() BC
BC![]() .
.
求四边形OABC 的面积, 其中 O 是原点
Answer :
10 unit