About Lesson
12.6 Distance from a Point to Line 点到直线的距离
(1)
Find the distance from the point (2, 3) to the line 7x – 24y + 8 = 0 and prove that the point(2, 3) and the origin are at the different side of the line.
Find the distance from the point (2, 3) to the line 7x – 24y + 8 = 0 and prove that the point(2, 3) and the origin are at the different side of the line.
求点(2, 3)到直线7x – 24y + 8 – 0的距离及证明点(2, 3)与原点在直线的两边.
Answer:
2
(2)
If P(h, k) is collinear with ( –2, 1), (1, 2), and the distance from P to the line 3x – 4y + 5 = 0 is 3 units, find the coordinate of P.
If P(h, k) is collinear with ( –2, 1), (1, 2), and the distance from P to the line 3x – 4y + 5 = 0 is 3 units, find the coordinate of P.
若点P(h, k)与(-2, 1), (1, 2)共线,及P与直线 3x – 4y + 5 = 0 之距离为3单位, 求P的座标。
Answer:
(10, 5), (-8, -1)
(3)
Find the equation of a straight line L, which is parallel to the line x + 2y –3 = 0 and the distance between them is 2 units.
Find the equation of a straight line L, which is parallel to the line x + 2y –3 = 0 and the distance between them is 2 units.
求和直线x + 2y – 3 = 0 平行且距离等于2的直线L的方程式。
Answer:
x + 2y – 3  2 = 0
2 = 0
(4)
Two parallel lines L : 2x + 2y – 1 = 0 and L
: 2x + 2y – 1 = 0 and L : 2x + 2y – 13 = 0.
: 2x + 2y – 13 = 0.
二平行线L : 2x + 2y – 1 = 0及L
: 2x + 2y – 1 = 0及L : 2x + 2y – 13 = 0.
: 2x + 2y – 13 = 0.
Two parallel lines L
二平行线L
(a) Find the y-intercept of L![]() .
.
求L![]() 之y截距.
之y截距.
(b) Find the distance between L![]() and L
and L![]() .
.
求L![]() 及L
及L![]() 之距离.
之距离.
(c) L![]() is another line parallel to L
is another line parallel to L![]() . If the distance between L
. If the distance between L![]() and L
and L![]() is equal to that between L
is equal to that between L![]() and L
and L![]() , find the equation of L
, find the equation of L![]() .
.
L![]() 为L
为L![]() 的另一平行线. 若L
的另一平行线. 若L![]() 与L
与L![]() 的距离和L
的距离和L![]() 与L
与L![]() 的距离相等, 求L
的距离相等, 求L![]() 之方程式.
之方程式.
Answer:
(a) 
(b) 3![]()
(c) 2x + 2y + 11 = 0
(5)
Find the equation of line which parallel with
which parallel with 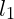 : 2x – 6y + 1 = 0 and
: 2x – 6y + 1 = 0 and  : x – 3y – 1 = 0, and separate
: x – 3y – 1 = 0, and separate 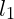 and
and 
求直线 之方程式使其与
之方程式使其与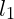 : 2x – 6y + 1 = 0 和
: 2x – 6y + 1 = 0 和 : x – 3y – 1 = 0平行, 且与
: x – 3y – 1 = 0平行, 且与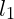 和
和
Find the equation of line
求直线
(a) internally to (內分) 1 : 2,
(b) externally to (外分) 1 : 3
Answer:
(a) x – 3y = 0
(b) 4x – 12y + 5 = 0
(6)
Given that the lines x + y + 3 = 0, x + 3y +7 = 0 and 2x + 3y + 5 = 0 form a triangle; find the heights of the triangle.
Given that the lines x + y + 3 = 0, x + 3y +7 = 0 and 2x + 3y + 5 = 0 form a triangle; find the heights of the triangle.
已知x + y+ 3 = 0, x + 3y + 7 = 0及2x + 3y + 5 = 0形成一三角形, 求其高
Answer:
(7)
ABCD is a trapezium where AB parallel to DC with the coordinates A(0,5), B(4,17), C(7, t), D(0, 0). Calculate the value of t and the distance of the two parallel lines.
ABCD is a trapezium where AB parallel to DC with the coordinates A(0,5), B(4,17), C(7, t), D(0, 0). Calculate the value of t and the distance of the two parallel lines.
ABCD为一梯形且AB与DC平行而座标A(0, 5), B(4, 17), C(7, t), D(0, 0). 求t之值及两平行线的距离.
Answer:
21 , 
(8)
Given that C(-1, 0) is the center of a square, x + 3y – 5 = 0 is the equation of one of its sides, find the equation of the other three sides.
Given that C(-1, 0) is the center of a square, x + 3y – 5 = 0 is the equation of one of its sides, find the equation of the other three sides.
已知C(-1, 0)为一正方形的中心, 一条边的方程式是x + 3y – 5 = 0, 求其他三边的方程式.
Answer:
3x – y – 3 = 0, 3x – y + 9 = 0, x + 3y + 7 = 0