About Lesson
16.2 Arithmetic Progression 等差数列
1.
Given that the 11 term of an arithmetic progression is 34, find the sum of the 3
term of an arithmetic progression is 34, find the sum of the 3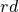 term, 9
term, 9 term and 21
term and 21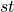 term.
term.
已知一等差数列的第11项是34,求第3项,第9项和第21项的和。
Given that the 11
已知一等差数列的第11项是34,求第3项,第9项和第21项的和。
Answer:
102

2.
Figure beside shows few circles where their radii increase by 1cm as follow on. Given that the total length of perimeter of the first five circles is 120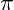 cm, find the length of radius for the smallest circle.
cm, find the length of radius for the smallest circle.
右图所示是一些圆,它们的半径依序增加1cm。已知首五个圆的圆周总长度是120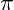 cm, 求最小的圆的半径。
cm, 求最小的圆的半径。
Figure beside shows few circles where their radii increase by 1cm as follow on. Given that the total length of perimeter of the first five circles is 120
右图所示是一些圆,它们的半径依序增加1cm。已知首五个圆的圆周总长度是120
Answer:
10 cm
3.
The n term of a arithmetic progression is represented as T
term of a arithmetic progression is represented as T and the sum of first n terms is represented as S
and the sum of first n terms is represented as S . Given that T
. Given that T + T
+ T = 40 and S
= 40 and S :S
:S = 2 : 3.
= 2 : 3.
T 表示一等差数列的第n项而 S
表示一等差数列的第n项而 S 表示首n项的和。已知 T
表示首n项的和。已知 T + T
+ T = 40 和 S
= 40 和 S :S
:S = 2 : 3.
= 2 : 3.
The n
T
(a) Calculate the value of the first term and the common difference.
计算首项和公差的值。
(b) Find the value of S![]() .
.
求S![]() 的值
的值
Answer:
(a) 5, 2
(b) 1020
4.
Figure beside shows three right angle triangle which has a fixed base and height decreasing 2 units as follow on.
右图为三个直角三角形,其底是固定长和高则依序减少2单位。
Figure beside shows three right angle triangle which has a fixed base and height decreasing 2 units as follow on.
右图为三个直角三角形,其底是固定长和高则依序减少2单位。
(a) Show that the area of the three triangles is an arithmetic progression.
试证该三个三角形的面积是一等差数列。
(b) If the areas of the following triangles have the same characteristic as above, given the total area of first six triangles is 1620cm![]() , find the area of the first triangle.
, find the area of the first triangle.
若接下来的三角形都有以上的性质,已知首六个三角形面积的和是1620 cm![]() ,求第一个三角形的面积。
,求第一个三角形的面积。
(c) Calculate the total area of all triangles that was formed.
试计算所能形成的三角形之总面积。
Answer:
(b) 300
(c) 3900cm![]()
5.
Find the sum of all integers divisible by 4 and 7, lying between 400 and 700.
求在400 和700 之间可以被4 和7 整除的整数之和。
Find the sum of all integers divisible by 4 and 7, lying between 400 and 700.
求在400 和700 之间可以被4 和7 整除的整数之和。
Answer:
5460
6.
Given that the first term, a and the common difference, d of an A.P. have the relation such that d – a = 1. If S = 610, S
= 610, S – S
– S = 30, where S
= 30, where S = T
= T + T
+ T + T
+ T + … +T
+ … +T and S
and S = T
= T + T
+ T + T
+ T + … +T
+ … +T = T
= T + T
+ T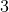 + … + T
+ … + T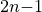 , find the values of a, d and n.
, find the values of a, d and n.
Given that the first term, a and the common difference, d of an A.P. have the relation such that d – a = 1. If S
已知一等差数列的首项,a和公差,d 使得d – a = 1. 若 S![]() = 610, S
= 610, S![]() – S
– S![]() = 30, 其中 S
= 30, 其中 S![]() = T
= T![]() + T
+ T![]() + T
+ T![]() + … +T
+ … +T![]() 和 S
和 S![]() = T
= T![]() + T
+ T![]() + T
+ T![]() + … +T
+ … +T![]() = T
= T![]() + T
+ T![]() + … + T
+ … + T![]() , 求 a, d 和n 的值.
, 求 a, d 和n 的值.
Answer:
2, 3, 10
7.
Given that in an A.P., the p term is 2000, the 2000
term is 2000, the 2000 term is p. Find the (2000 + p)
term is p. Find the (2000 + p) term.
term.
已知一等差数列,第p 项是 2000, 第2000 项是 p. 求第 (2000 + p)项。
Given that in an A.P., the p
已知一等差数列,第p 项是 2000, 第2000 项是 p. 求第 (2000 + p)项。
Answer:
0