About Lesson
16.4 Infinite Series 无穷级数
1.
State the recurring decimal . in the fraction form.
. in the fraction form.
把循环小数 换成分数式。
换成分数式。
State the recurring decimal
把循环小数
Answer:
2.
Find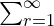
 , expressing your answer as a fraction in its lowest terms. Hence, or otherwise, express the infinite recurring decimal
, expressing your answer as a fraction in its lowest terms. Hence, or otherwise, express the infinite recurring decimal  0
0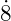 as a fraction in its lowest terms.
as a fraction in its lowest terms.
Find

Answer:
![]()
3.
Each time that a ball falls vertically on to a horizontal floor it rebounds to three-quarters of the height from which it fell. It is initially dropped from a point 4m above the floor. Find, and simplify, an expression for the total distance the ball travels until it is about to touch the floor for the nth time. Hence find the number of times the ball has bounced when it has traveled 24m and also the total distance it travels before coming to rest. (The dimensions of the ball are to be ignored.)
Each time that a ball falls vertically on to a horizontal floor it rebounds to three-quarters of the height from which it fell. It is initially dropped from a point 4m above the floor. Find, and simplify, an expression for the total distance the ball travels until it is about to touch the floor for the nth time. Hence find the number of times the ball has bounced when it has traveled 24m and also the total distance it travels before coming to rest. (The dimensions of the ball are to be ignored.)
每次球垂直落到水平地板上时,它会反弹到落下高度的四分之三。它最初从地板上方 4m 的点掉落。找出并简化球在第 n 次触地前所经过的总距离的式子。据此,求球在移动 24m 后经过的弹跳次数以及它在静止之前移动的总距离。 (球的尺寸忽略。)
Answer:
28 – 32 , 7 , 28
, 7 , 28
4.
A ball is thrown vertically to height 80m. Each time the ball falls it is rebounded by the floor, the height that it will reach is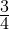 of the previous height.
of the previous height.
一球垂直向上抛至80米高。每次该球落地反弹是之前高度的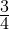 。
。
A ball is thrown vertically to height 80m. Each time the ball falls it is rebounded by the floor, the height that it will reach is
一球垂直向上抛至80米高。每次该球落地反弹是之前高度的
(a) Find after how many bounce that the ball has the height less than 10m.
请问该球经过多少次的反弹后其高度会少过10米。
(b) Calculate the total distance that traveled by the ball before it stop.
试计算球在静止之前经过的总距离。
Answer:
(a) 8
(b) 640m