16.5 The Sum of Some Simple Progression 简易特殊数列的和
Calculate the sum of the following series
计算下列各级数的和
2 x (-2) + 5 x 2 + 10 x 6 + 17 x 10 + . . . + (n![]() + 1)(4n – 6)
+ 1)(4n – 6)
Answer:
1 x 1 + (-1) x 5 + (-3) x 9 + (-5) x 13 + …. + (-37) x 77
Answer:
2![]() x 2 + 3
x 2 + 3![]() x 5 + 4
x 5 + 4![]() x 8 + 5
x 8 + 5![]() x 11 + … + 11
x 11 + … + 11![]() x 29
x 29
Answer:
1 x 4 x 7 + 2 x 5 x 8 + 3 x 6 x 9 + … + 10 x 13 x 16
Answer:
18![]() – 17
– 17![]() + 16
+ 16![]() – 15
– 15![]() + 14
+ 14![]() – 13
– 13![]() + … + 2
+ … + 2![]() – 1
– 1![]()
Answer:
1 + ![]() +
+ ![]() +
+ ![]() + …
+ …
Answer:
1 + ![]() +
+ ![]() +
+ ![]() +
+ ![]()
Answer:
1 + ![]() +
+ ![]() +
+ ![]() +
+ ![]() to n term(至第n项)
to n term(至第n项)
Answer:
9.
1 + (1 + a)r + (1 + a + a![]() )r
)r![]() + (1 + a + a
+ (1 + a + a![]() + a
+ a![]() )r
)r![]() + … where(其中) |ar| < 1.
+ … where(其中) |ar| < 1.
Answer:
*** QuickLaTeX cannot compile formula:
\[ \sum_{i=0}^{\infty}\frac{3i+2}{5^i}
*** Error message:
Missing $ inserted.
leading text: \end{document}
Answer:
![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]()
Answer:
![]() +
+ ![]() +
+ ![]() +
+ ![]()
Answer:
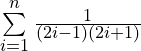
Answer:
![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]()
Answer:
Simplify ![]() (3n – 2)
(3n – 2)![]() . Hence, find the value of 732 + 762 + 792 + … + 2082 .
. Hence, find the value of 732 + 762 + 792 + … + 2082 .
化简![]() (3n – 2)
(3n – 2)![]() . 据此, 求 732 + 762 + 792 + … + 2082 的值。
. 据此, 求 732 + 762 + 792 + … + 2082 的值。
Answer:
Define a series such that, the first term is 3, the second term is 3 + 8, the third term is 3 + 8 + 13, the fourth term is 3 + 8 + 13 + 18 and so on. Find the sum of the first n terms of this series.
一级数其首项是3, 第二项是 3 + 8, 第三项是 3 + 8 + 13, 第四项是 3 + 8 + 13 + 18 以此类推。求这个级数首n 项的和。