About Lesson
Decompose the following fractions into partial fractions
把下列分式分成部分分式
把下列分式分成部分分式
(1) ![]()
(2) 
(3) ![]()
(4) 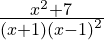
(5) 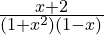
(6) ![]()
(7) ![]()
(8) 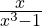
(9) 
(10) 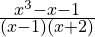
(11) ![]()
(12)  [bg_collapse view=”link” color=”#4a4949″ expand_text=”Hint” collapse_text=”Closed Hint” ]
[bg_collapse view=”link” color=”#4a4949″ expand_text=”Hint” collapse_text=”Closed Hint” ]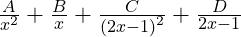 [/bg_collapse]
[/bg_collapse]
(13)  | [bg_collapse view=”link” color=”#4a4949″ expand_text=”Hint” collapse_text=”Closed Hint” ]
| [bg_collapse view=”link” color=”#4a4949″ expand_text=”Hint” collapse_text=”Closed Hint” ] , 令x= 0找A,用比较系数法找其他。[/bg_collapse]
, 令x= 0找A,用比较系数法找其他。[/bg_collapse]
Answer 答案:
(1) 
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
(6) ![]()
(7) ![]()
(8) ![]()
(9) ![]()
(10) ![]()
(11) ![]()
(12) ![]()
(13) ![]()