About Lesson
(1)
Convert the following trigonometric functions to acute trigonometric functions.
化下列各三角函数为锐角三角函数
(a)
(b)
(c)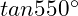
(d) )
)
(e)
(f)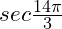
Convert the following trigonometric functions to acute trigonometric functions.
化下列各三角函数为锐角三角函数
(a)
(b)
(c)
(d)
(e)
(f)
答案 Answer
(a) 
(b)
(c)
(d)
(e)
(f)
(b)
(c)
(d)
(e)
(f)
(2)
Given that
Given that
*** QuickLaTeX cannot compile formula:
tanA= \frac{8}{15}
*** Error message:
Unicode character (U+2061)
leading text: $tan
, where ![]() is in the third quadrant, calculate
is in the third quadrant, calculate ![]() and
and ![]()
已知
*** QuickLaTeX cannot compile formula:
tanA= \frac{8}{15}
*** Error message:
Unicode character (U+2061)
leading text: $tan
, 且A 在第三象限, 计算 ![]() 和
和 ![]() 。
。
答案 Answer
(3)
Given that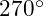 <
<  <
< 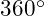 , and
, and  , find the value of
, find the value of
Given that
*** QuickLaTeX cannot compile formula:
\frac{13 sinA+5 secA}{3 tanA+cose A}
*** Error message:
Unicode character (U+2061)
leading text: $\frac{13 sinA+5 secA}{3 tanA+cose A}
已知![]() <
< ![]() <
< ![]() 以及
以及 ![]() , 求
, 求
*** QuickLaTeX cannot compile formula:
\frac{13 sinA+5 secA}{3 tanA+cose A}
*** Error message:
Unicode character (U+2061)
leading text: $\frac{13 sinA+5 secA}{3 tanA+cose A}
的值
答案 Answer
(4)
If , calculate the values of
, calculate the values of 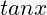 and
and  .
.
若 , 试计算
, 试计算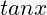 和
和 的值。
的值。
If
若
答案 Answer
(5)
If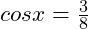 , calculate the values of
, calculate the values of 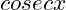 .
.
若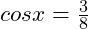 , 求
, 求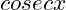 的值.
的值.
If
若
答案 Answer
![]() 当
当![]() 在第四象限
在第四象限
(6)
If 12tan x = 5, sin x < 0, calculate the value of
If 12tan x = 5, sin x < 0, calculate the value of
*** QuickLaTeX cannot compile formula:
\frac{2sinx+secx}{4 cotx-3 cosx}
*** Error message:
Unicode character (U+2061)
leading text: $\frac{2sinx+secx}{4 cotx-3 cosx}
若 12tan x = 5, sin x < 0, 求
*** QuickLaTeX cannot compile formula:
\frac{2sinx+secx}{4 cotx-3 cosx}
*** Error message:
Unicode character (U+2061)
leading text: $\frac{2sinx+secx}{4 cotx-3 cosx}
的值。