About Lesson
9.1 Basic Trigonometric Identities 基本三角关系式
1. Prove that 试证
(a) ![]()
(b)
*** QuickLaTeX cannot compile formula:
\frac{1-tan^2x}{1+tan^2x} = 1-2 〖sin〗^2x
*** Error message:
Unicode character (U+2061)
leading text: $\frac{1-tan^2x}{1+tan^2x}
(c) 
(d) 
(e) 
(f) 
(g) 
(2)
If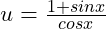 , prove that
, prove that 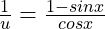
If
若 ![]() , 证明
, 证明 ![]()
(3)
If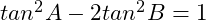 , show that
, show that 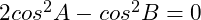
If
若 ![]() , 证明
, 证明 ![]()
(4)
If , find the values of
, find the values of
若 , 求下列各式的值
, 求下列各式的值
(a) sin A cos A
(b) tan A + cot A
If
若
(a) sin A cos A
(b) tan A + cot A
Answer 答案:
(a) 
(b) ![]()
(5)
If , then find the value of
, then find the value of 
若 则求
则求  之值
之值
If
若
Answer 答案:
(6)
Given that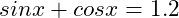 , find
, find  , if
, if 
已知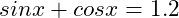 , 求
, 求  , 当
, 当 
Given that
已知
Answer 答案:
(7)
Given that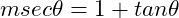 ,
, 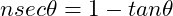 , prove that
, prove that  .
.
Given that
已知 ![]() ,
, ![]() , 证明
, 证明 ![]() .
.
(8)
If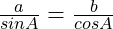 show that
show that 
If
若 ![]() 证明
证明 ![]()