About Lesson
(1)
Given that , where
, where 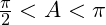 ;
;  , where
, where 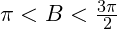 , find the value of
, find the value of  .
.
已知 , 且
, 且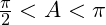 ; , 且
; , 且 , 求
, 求  的值.
的值.
Given that
已知
Answer:
(2)
Prove that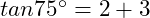
证明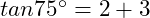
Prove that
证明
(3)
Show that, if ,
, 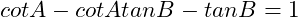
试证,若 ,
, 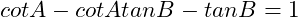
Show that, if
试证,若
(4)
If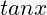 and
and 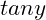 are the roots of equation
are the roots of equation  , find the value of
, find the value of  .
.
若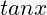 及
及 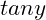 为方程式
为方程式 的根, 求
的根, 求 的值.
的值.
If
若
Answer:
(5)
If A + B = 90
If A + B = 90
*** QuickLaTeX cannot compile formula:
^{\cirl}
*** Error message:
Undefined control sequence \cirl.
leading text: $^{\cirl
and A > 0
*** QuickLaTeX cannot compile formula:
^{\cirl}
*** Error message:
Undefined control sequence \cirl.
leading text: $^{\cirl
, B > 0
*** QuickLaTeX cannot compile formula:
^{\cirl}
*** Error message:
Undefined control sequence \cirl.
leading text: $^{\cirl
, prove that tan A tan B = 1.
Hence without using calculator or mathematical tables, find the value of tan 75
*** QuickLaTeX cannot compile formula:
^{\cirl}
*** Error message:
Undefined control sequence \cirl.
leading text: $^{\cirl
– tan15
*** QuickLaTeX cannot compile formula:
^{\cirl}
*** Error message:
Undefined control sequence \cirl.
leading text: $^{\cirl
.
若A + B = 90
*** QuickLaTeX cannot compile formula:
^{\cirl}
*** Error message:
Undefined control sequence \cirl.
leading text: $^{\cirl
和 A > 0
*** QuickLaTeX cannot compile formula:
^{\cirl}
*** Error message:
Undefined control sequence \cirl.
leading text: $^{\cirl
, B > 0
*** QuickLaTeX cannot compile formula:
^{\cirl}
*** Error message:
Undefined control sequence \cirl.
leading text: $^{\cirl
, 证明 tan A tan B = 1.
据此不用计算机或查表,求 tan 75
*** QuickLaTeX cannot compile formula:
^{\cirl}
*** Error message:
Undefined control sequence \cirl.
leading text: $^{\cirl
– tan15
*** QuickLaTeX cannot compile formula:
^{\cirl}
*** Error message:
Undefined control sequence \cirl.
leading text: $^{\cirl
的值.
Answer:
Prove the following identities.
证明下列恒等式
证明下列恒等式
(6)
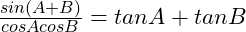
(7)
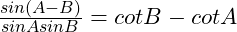
(8)
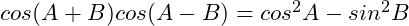
(9)
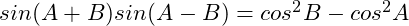
(10)

(11)

(12)
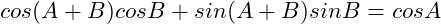
(13)
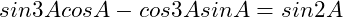
(14)

(15)

(16)
Prove that in triangle
试证在三角形ABC中,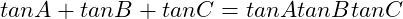
Prove that in triangle
试证在三角形ABC中,