About Lesson
(1) Prove the following identities
证明下列恒等式
(a) 
(b) 
(c) 
(d) 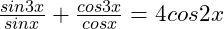
(e) 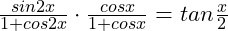
(f) 
(g) 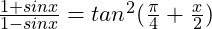
(h) 
(i) 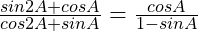
(j) 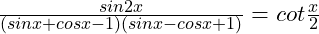
(2)
If ![]() ,
, ![]() and
and ![]() ; find without using calculator or tables, the values of
; find without using calculator or tables, the values of
若![]() ,
, ![]() 和
和 ![]() ; 不用计算机或查表,求
; 不用计算机或查表,求
(a) ![]()
(b) ![]()
(c) ![]()
Answer 答案:
(a) 
(b)
(c)
(b)
(c)
(3)
Given that , find the values of a, b and c.
, find the values of a, b and c.
已知 , 求 a, b 和 c的值.
, 求 a, b 和 c的值.
Given that
已知
Answer 答案:
![]() ,
, ![]() ,
, ![]()