About Lesson
(1) Prove that 证明
(a)
*** QuickLaTeX cannot compile formula: cosx + 2cos3x + cos5x$ = $4cos^2x\cos3x *** Error message: Unicode character 3 (U+FF13) leading text: $cosx + 2cos3
(b) ![]()
(c) ![]() =
= ![]()
(d) ![]() =
= ![]()
(e) ![]() =
= ![]()
(2) In triangle ABC, prove that 在三角形ABC中, 证明
(a) ![]() =
= ![]()
(b) ![]() =
= ![]()
(c) ![]() =
= ![]()
(3) Without using any calculator or tables, find the value of
不用计算机或查表,求下列各式的值
(a) ![]()
(b) ![]()
Answer
(a) 
(b) ![]()
(4) If ![]() , show that
, show that ![]()
若![]() , 试证
, 试证 ![]()
(5)
Prove that . If
. If 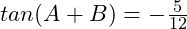 and
and  , where
, where  and
and 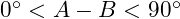 . Find
. Find 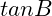
Prove that
证明 ![]() . 若
. 若 ![]() 和
和 ![]() , 且
, 且 ![]() 及
及 ![]() . 求
. 求 ![]()
Answer
(6) If ![]() , prove that
, prove that ![]() =
= ![]()
若 ![]() , 试证
, 试证 ![]() =
= ![]()
(7) If ![]() and
and ![]() , find the value of
, find the value of ![]()
若 ![]() 及
及 ![]() , 求
, 求 ![]() 的值。
的值。
Answer
![]()
(8) Given that  ,
,  , find the value of
, find the value of
已知 ![]() ,
, ![]() , 求下列各式的值
, 求下列各式的值
(a) ![]()
(b) ![]()
(c) ![]()
Answer
(a) 
(b) ![]()
(c) ![]()
(9) Find the value of  +
+ +
+ +
+
求 ![]() +
+![]() +
+![]() +
+![]() 的值。
的值。
Answer
1